This note is based on Coursera course by Andrew ng.
(It is just study note for me. It could be copied or awkward sometimes for sentence anything, because i am not native. But, i want to learn Deep Learning on English. So, everything will be bettter and better :))
To get us familiar with these ideas, it will make a bit more sense when we walk about full-fledged neural networks. To that, let's dive into gradient descent for logistic regression.

The first thing we want to do when going bacakwards is to conpute the derivative of this loss with respect to a. And we can show that dz is equal to a - y. Then, the final step in that computation is to go back to compute how much you need to change w and b. In particular, we can show that the derivative with respect to w1 is equal to x1*dz. Then, similarly, dw2 is how much you want to change w2, x2 * dz. And db is equal to dz.
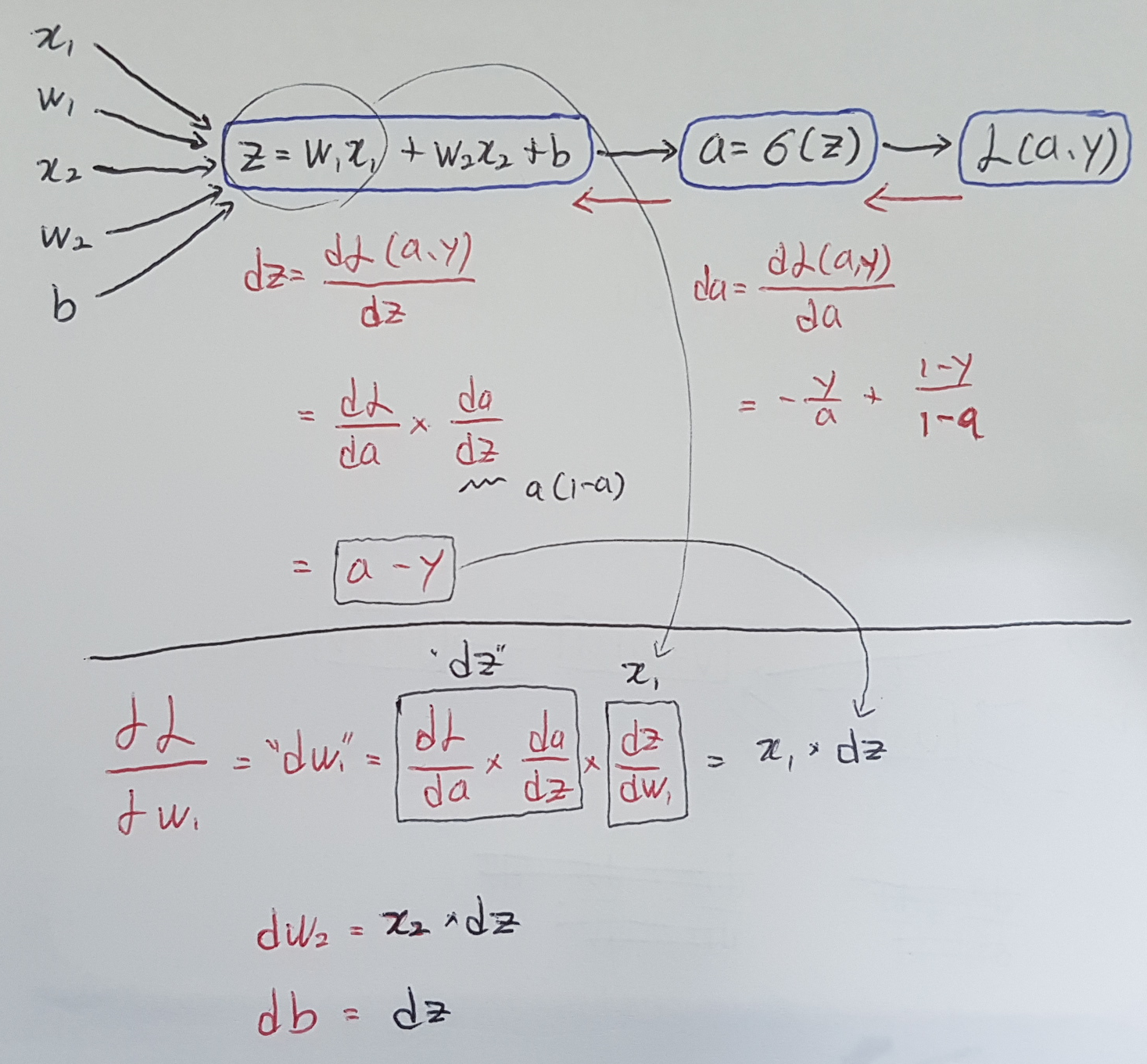
Okay, this is gradient descent with respect to just one training example for logistic regression. Now, we want to do it for m training examples. Let's remind ourselves of the definition of the cost function J. The derivative respect to w1 of the overall cost function is also going to be the average of derivatives respect to w1 of the individual lost terms. Let's take all of this upand wrap this up into a concrete algorithm until when you should implement logistic regression with gradient descent working.

(Just in case you don't understand why the for loop is configured like the below, we use this simple network.)

Let's initialize J=0, dd1=0, dw2=0 and b=0. What we are going to do is user for loop over the training set. And compute the derivative with respect to each training example and then add them up. Then finally, having done this for all m training examples, we will need to divide by m because we are computing averages.
We are using dw1, dw2 and db as accumulators. To implement one step of gradient descent after that computation, we will implement w1, gets updated as w1 minus the learning rate times dw1, dw2, ends up this as w2 minus learning rate times dw2, b, gets updated as b minus learning rate times db, where dw1, dw2 and db were as computed.
So, everything on this image below implements just one single step of gradient descent.

However it turns out there are two weaknesses with the calculation as we have implemented it here. It means that we need to write two for loops to implement logistic regression this way. First for loop is for loop over the m training examples, and the second for loop is a for loop over all the features over there.

When you are implementing deep learning algorithms, you find that having explicit for-loops in your code makes your algorithm run less efficiency. So, it turns out that there are a set of techniques called vectorization techniques that allow you to get rid of these explicit for-loops in your code.