2213번: 트리의 독립집합
첫째 줄에 트리의 정점의 수 n이 주어진다. n은 10,000이하인 양의 정수이다. 1부터 n사이의 정수가 트리의 정점이라고 가정한다. 둘째 줄에는 n개의 정수 w1, w2, ..., wn이 주어지는데, wi는 정점 i의
www.acmicpc.net
알고리즘 종류
트리
다이나믹 프로그래밍
사고 과정
이 문제는 제가 바로 이전에 풀어보았던 문제와 유사했습니다. 독립집합이 되기 위해서는 A가 선택되면 연결된 다른 노드들은 선택되면 안됩니다. 반대로, A가 선택되지 않으면 연결된 다른 노드들은 선택되거나 선택되지 않아야 됩니다. 이러한 문제를 독립집합이라고 하는 것 같습니다. 따라서 제가 배운 DP로 풀면 될 것 같습니다.
조건은 다음과 같습니다.
- A가 선택되면, 연결된 다른 노드들은 선택할 수 없다.
- A가 선택되지 않으면, 다른 노드들은 선택되거나 선택되지 않아도 된다.
가장 먼저 Root가 될 노드를 찾기로 했습니다. 연결된 간선이 1개면 됩니다. 그리고 DP를 수행하여 최대 독립집합을 구했습니다. 마지막으로 최대 독립집합의 노드들을 구하기 위해서 Root부터 시작하여 DP의 크기를 비교하면서 노드들을 찾았습니다. 구체적인 내용은 아래 코드를 보면 쉬울 것 입니다.
과정을 이미지로 나타내면 아래와 같습니다. 빨간색은 가중치, 화살표는 DP가 수행되는 방향 입니다.
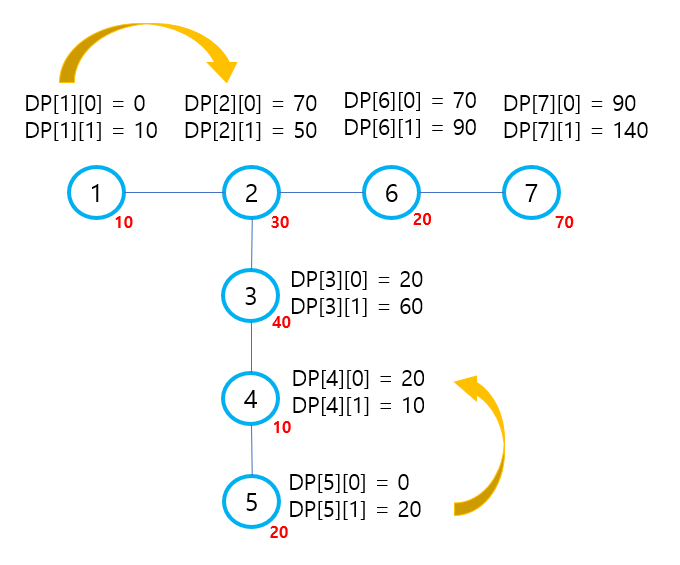
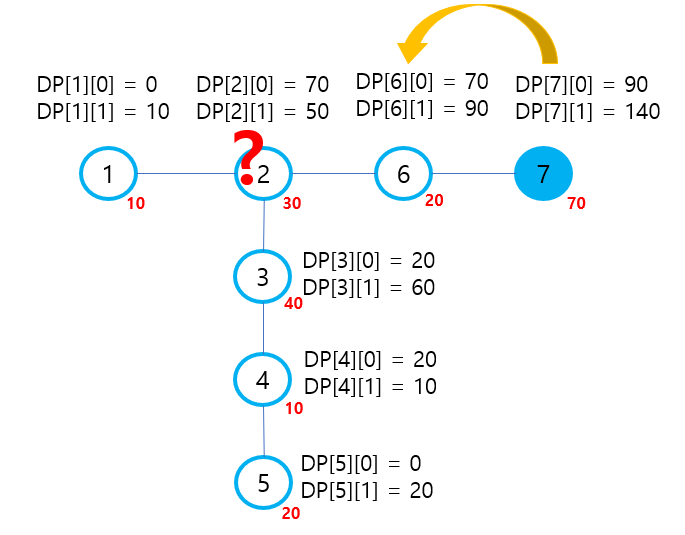
노드들을 추적하는 이미지는 아래와 같습니다. DP를 통해 7번 노드는 포함되는 것이 최대값입니다. 그러면 6번 노드는 당연히 포함되지 않습니다. 그러면 2번 노드는 어떻게 할까요? DP를 통해서 DP[2][0] = 70 VS DP[2][1] = 50 이므로 포함시키지 않는 것이 최대값입니다.
구현(C++)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
|
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int dp[10001][2];
int isVisited[10001];
vector<vector<int> > edges; // 노드 연결된 간선 정보
vector<int> weights; // 노드의 가중치
vector<int> nodes; // 노드에 간선이 몇 개 연결되어 있는지. 간선이 1개 있는 노드에서 DP 시작하기 위해서
vector<int> set; // 최대 독립 집합에 속한 노드들 저장
// 최대 독립집합의 크기 구하기
void dfs(int node){
isVisited[node] = 1;
dp[node][0] = 0;
dp[node][1] = weights[node];
for(int i=0; i<edges[node].size(); i++){
int conn_node = edges[node][i];
if(isVisited[conn_node]) continue;
dfs(conn_node);
dp[node][0] += max(dp[conn_node][0], dp[conn_node][1]);
dp[node][1] += dp[conn_node][0];
}
}
// 최대 독립 집합에 속한 노드들 구하기
void track(int node, bool check){
isVisited[node] = 1;
// 현재 노드가 속하면, 배열에 넣어준다.
if(check){
set.push_back(node);
for(int i=0; i<edges[node].size(); i++){
int conn_node = edges[node][i];
if(isVisited[conn_node]) continue;
track(conn_node, false);
}
}
// 현재 노드가 속하면, 다음 노드를 선택하거나 아니거나.
else{
for(int i=0; i<edges[node].size(); i++){
int conn_node = edges[node][i];
if(isVisited[conn_node]) continue;
// 최대 가중치만 DP에 저장했으므로 값이 큰 쪽으로 따라간다.
if(dp[conn_node][0] > dp[conn_node][1])
track(conn_node, 0);
else
track(conn_node, 1);
}
}
}
int main(void){
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin >> n;
edges.resize(n+1);
weights.resize(n+1);
nodes.resize(n+1);
int w;
for(int i=1; i<=n; i++){
cin >> w;
weights[i] = w;
}
int u, v;
while(cin >> u >> v){
edges[u].push_back(v);
edges[v].push_back(u);
nodes[u]++;
nodes[v]++;
}
// 간선이 1개 있는 노드 찾기
int root;
for(int i=1; i<=n; i++){
if(nodes[i] == 1) root = i;
}
// 최대 독립집합 구하기
dfs(root);
cout << max(dp[root][1], dp[root][0]) << endl;
// 최대 독립집합의 노드들 구하기
memset(isVisited, 0, sizeof(isVisited));
if(dp[root][1] > dp[root][0]) track(root, true);
else track(root, false);
sort(set.begin(), set.end());
for(int i=0; i<set.size(); i++) cout << set[i] << " ";
}
|
cs |
시행착오
이 문제를 풀기 전에 이와 비슷한 유형의 문제를 풀었습니다. 배운 내용을 바로 적용해 볼 수 있어서 풀면서 재미를 느꼈습니다.
'코딩 공부 > 백준' 카테고리의 다른 글
| [백준][C++] 13911 집 구하기 (0) | 2021.04.01 |
|---|---|
| [백준][C++] 1949 우수 마을 (0) | 2021.03.31 |
| [백준][C++] 2533 사회망 서비스(SNS) (2) | 2021.03.31 |
| [백준][C++] 2250 트리의 높이와 너비 (0) | 2021.03.31 |
| [백준][C++] 17244 아맞다우산 (0) | 2021.03.31 |