This note is based on Coursera course by Andrew ng.
(It is just study note for me. It could be copied or awkward sometimes for sentence anything, because i am not native. But, i want to learn Deep Learning on English. So, everything will be bettter and better :))
INTRO
Batch normalization makes hyperparameter search problem much easier and makes neural network much more robust. The choice of hyperparameters is a much bigger range of hyperparameters that work well, and will enable us to much more easily train very deep networks.
What batch normalization does is it applies that normalization process not just to the input layer, but to the values even deep in some hidden layer in the neural network. So, it will apply this type of normalization to normalize the mean and variance of some of hidden units' values, z[l].
MAIN
WHAT
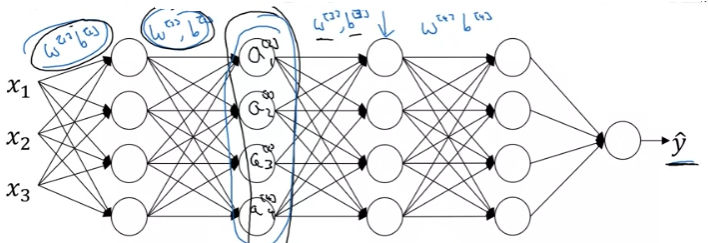
We did normalize the input feature values to a neural network. How about a deeper model? We have not just input features x, but in the layers we have many activations. We normalize the value of z[l], so as to train w[l+1] faster.

Given some intermediate values in neural net, z[1] ~ z[m], we compute the mean as follows:

Now we have taken these values z and normalize them to thave mean 0 and standard unit variance. So, every component of z has mean 0 and variance 1. But, we don't want the hidden units to always have mean 0 and variance 1. It takes sense for hidden units to have a different distribution.
We would update the parameters gamma and beta, just as we would update the weights of neural network. The effect of gamma and beta is that it allows us to set the mean of z~[l](i) to be whatever we want it to be. If we look at the z~[l](i), it exactly invert the z(i)norm equation.

So, by appropriate setting of the parameters gamma and beta, the normalization step is computing essentially the identity function. But by choosing other values of gamma and beta, the normalization allows us to make the hidden unit values have other means and variances as well.
HOW
How does it fit into the training of a deep network? We take this value Z[1], and apply batch norm, and this will give use the new normalized value Z[1], and then we fit that to the activation function to get A[1], and so on. For clarity, that β here is different from hyperparameter β from momentum.

Now, there is one detail to the perameterization that we should clean up. If we look at the mini-batch and normalize Z[l], and then a rescale by β and Γ. It means that whatever is the value of b[l] is actually going to just get substracted out. Because during batch normalization step, we are going to compute the means of the Z[l] and subtract the mean. So, adding any constant to all of the examples in the mini-batch, it doesn't change anything, because any constant will get cancelled out by the mean subtraction step. If we are using batch norm, we can actually eliminate that parameter b.

Okay, let's put all together and describe how we can implement gradient descent using batch norm. Assuming we are using mini-batch gradient descent:

WHY
Why does Batch Norm work? We have seen how normalizing the input features X to mean 0 and variance 1 and that could speed up learning. So rather than having some features that range from 0 to 1 and some from 1 to 1000, by normalizing all the features, input X, to take on a similar range of values that can speed up learning. So, one intuition behind why Batch norm works is that this is doing a similar thing. There are a couple of futher intuitions, that will help us to gain a deeper understanding of what Batch norm is doing.
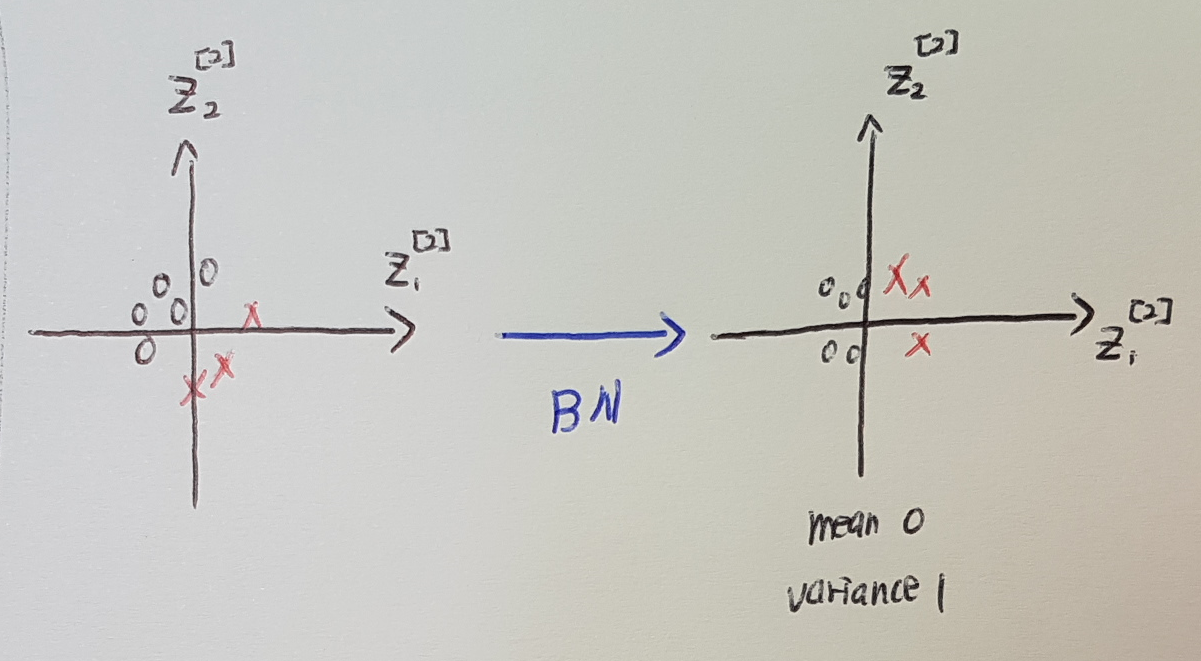
Let's go with simple example. we are training black cat images. If we try to apply this network to data with colored cats, then our classifier might not do very well.

If we plot the training set, it looks like left. But we try to generalize it to colored cats. Then we might not expect a module trained on the data on the left to do well on the data on the right.

Even though there might be the same function that actually works well. But we wouldn't expect our algorithm to discover that green decision boundry, just looking at the data on the left.

So, this idea of data distribution changing goes by the somewhat fancy name, covariate shift. The idea is if we have learned some X to Y mapping, if the distribution of X changes, then we might need to retrain our learning algorithm. How does this problem of covariate shift apply to a neural network?
Consider a deep network and look at the learning process from the perspective of third layer.

And let's cover up the left side of third layer. The third hidden layer gets some values, a[2][1], a[2][2], a[2][3], a[2][4]. The job of third hidden layer is to take these values and find a way to map them to Y_hat.

But now let's uncover the left of the network. The network is adapting parameters W[2], b[2], W[1], b[1]. So as these parameters chagnes, the values a[2] will also change. So, it is suffering from the problem of covariate shift. So! what Batch norm does is it reduces the amount that the distribution of these hidden unit values shift around.
The values for z[2][1] and z[2][2] can change, and they indeed will change when the neural network updates the parameters W[1], b[1], W[2], b[2], ... in the earlier layers. But, what Batch norm ensures is that no matter how it changes, the mean and variance of z[2][1] and z[2][2] will remain the same. They will at least stay at same mean 0 and variance 1, or whatever value is governed by beta and gamma.
Regularization effect
Each mini-batch is scaled by the mean and variance computed on just that mini-batch. This adds some noise to the values Z[l] within that mini-batch. Because it is computed just on mini-batch of 64, or 128, ... It means that it is estimated with a relatively small sample of data and scaled by standard deviation. Similar to dropout, it adds some noise to each hidden layer's activations. So, Batch norm has a slight regularization effect. But, it is just slight side effect, so don't turn to Batch norm as a regularization.
CONCLUSION