This note is based on Coursera course by Andrew ng.
(It is just study note for me. It could be copied or awkward sometimes for sentence anything, because i am not native. But, i want to learn Deep Learning on English. So, everything will be bettter and better :))
INTRO
People used to worry a lot about the optimization algorithm getting stuck in bad local optima.
MAIN
This is a picture people used to have in mind when they worried about local optima. In this picture, it looks like there are a lot of local optima. And it would be easy for gradient descent to get stuck in a local optimum rather than find its way to a global optimum.

But this intuition isn't actually correct. It turns out if we create a neural network, most points of zero gradients are not local optima like points like above. Instead most points of zero gradient in a cost function are saddle points. At the saddle point, some directions can be curving down instead we are much more likely to get some directions where the curve bends upwards.
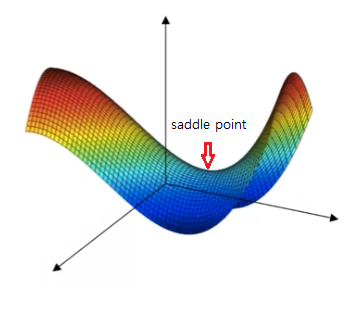

If local optima is not a problem, then what is a problem? It turns out that plateaus can slow down learning and a plateau is a region where derivative is close to zero for a long time. So, gradient descent will take a very long time to slowly find way to optimum.

CONCLUSION
Problem
- Unlikely to get stuck in a bad local optima.
- Plateaus can make learning slow.