Hash table
- 키(key)값에 해시값(hash value)를 연관지어 저장하는 자료구조
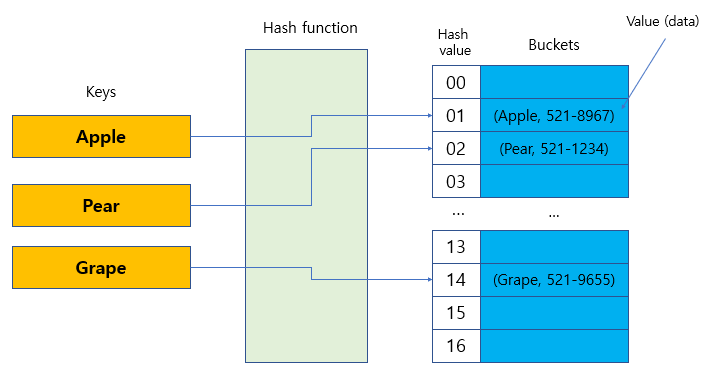
용어 표현
- Hash function : 임의의 길이를 갖는 임의의 데이터에 대해 고정된 길이의 데이터로 매핑하는 함수
- 해싱(Hashing) : 데이터를 매핑하는 과정
- 키(key) : 매핑 전 원래 데이터 값
- 해시값(hash value) : 해시 함수를 적용하여 나온 고정된 길이의 값
- bucket : 데이터가 저장되는 공간
- 값(value) : 데이터 값
장점
- 광대한 데이터를 유한한 해시값으로 매핑하므로써 작은 크기의 캐쉬 메모리로도 프로세스를 효율적으로 관리 * How? Hash function으로 임의의 데이터를 고정된 길이의 데이터로 매핑하기 때문이다.
- 탐색에 index로 hash value를 사용하기 때문에 간단한 연산으로 데이터에 빠르게 접근 가능
* 삽입/삭제/탐색 시간복잡도 : O(1)
* 이진 트리의 경우 시간복잡도 : O(logN)
* 배열의 경우 시간복잡도 O(1), 하지만 공간을 추가로 차지
- 보안에서 사용 : 키와 해시값 사이의 직접적인 연관성이 없기 때문에 하나만 알아서는 다른 하나를 알기 어려움
단점
- 순서가 있는 데이터에는 어울리지 않음
- 해시함수에 의존도가 높아서 해시함수에 따라 시간 효율성이 달라질 수 있음
삽입
- 해시 함수가 할당 받은 키 값을 x값으로 나누어서 남은 값을 해시값으로 하여 저장
- 예시 (선형 탐사)
* 첫 번째 예시 : 키값 32를 8로 나누고 나온 해시값 0에 값(A)를 저장
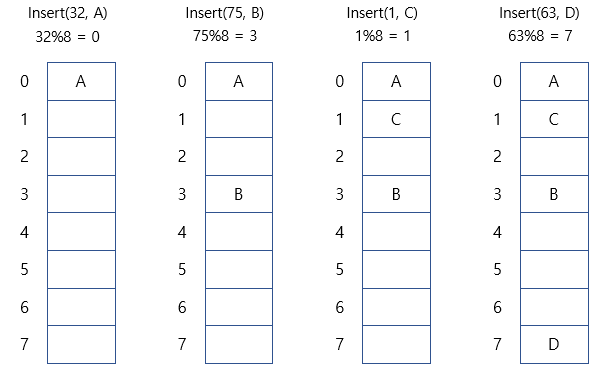
- 문제 : 해시충돌
- 삽입 시간복잡도 : O(1)
- 해시충돌이 일어날 경우, 최악의 경우 : O(n)
삭제
- 해당 키값과 매칭이 되는 값을 삭제
- 간단함
- 삭제 시간복잡도 : O(1)
- 해시충돌이 일어날 경우, 최악의 경우 : O(n)
해시충돌
- 해시함수는 많은 키값을 해쉬값으로 변환하기 때문에 서로 다른 키값이 동일한 해키값을 가지게 될 수도 있다. 이때를 해시 충돌이라고 한다.

해시충돌 해결
1) Chaining
- 연결 리스트를 이용하여 버켓에 노드를 추가하는 방법
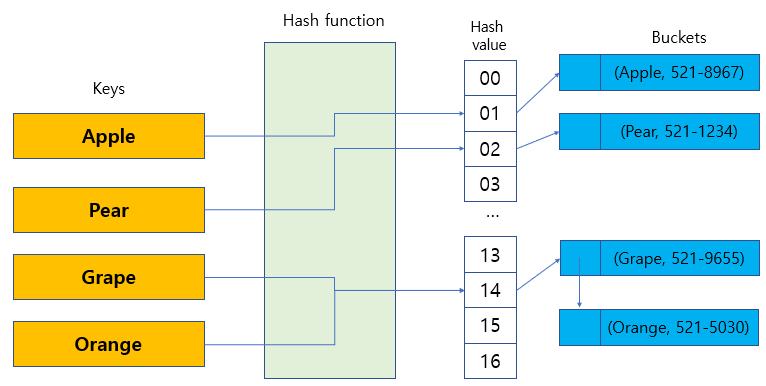
- 삽입/탐색/삭제 시작복잡도
* 가정 : 테이블의 크기가 m이고 키의 개수가 n 일 때, bucket에 들어가는 평균 데이터 개수는 n/m = a 개
* 삽입 시간복잡도 : O(1)
+ 키값을 해시값으로 매핑하는 데 O(1) + 연결 리스트를 추가하는 데 O(1) = O(1)
* 탐색 시간복잡도 : O(1 + a)
+ 키값을 해시값으로 매핑하는 데 O(1) + 해당 bucket을 찾아보는 데 O(a) = O(1 + a)
* 삭제 시간복잡도 : O(1 +a )
+ 키값을 해시값으로 매핑하는 데 O(1) + 해당 bucket을 찾아보는 데 O(a) + 삭제하는 데 O(1) = O(1 + a)
- 단점
* 메모리 문제
- 장점
- 해시충돌 발생하지 않음
2) Open addressing
- 해시충돌이 일어날 경우, 다른 bucket에 데이터를 매핑하여 저장하는 방법
- 예시
* 2번째에서 hash value = 2에서 해시충돌이 발생하여 옆의 빈 공간으로 B 할당
* 4번째에서 hash value = 2에서 해시충돌이 발생하여 옆의 빈 공간으로 D 할당
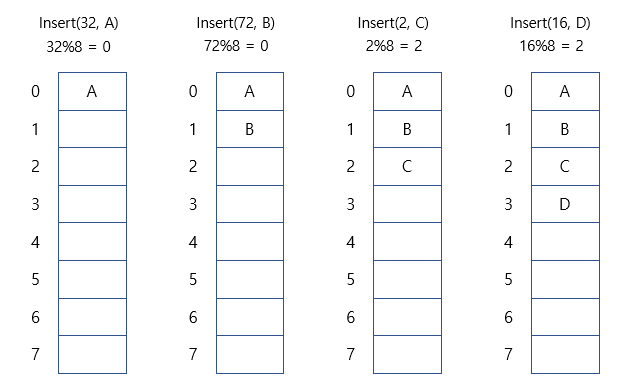
- 비어있는 해시값을 찾는 방법
* 선형 탐사(Linear probing) : 해시충돌이 일어났을 때, 고정된 칸 수 만큼 이동하여 데이터 저장
+ 위에 예시가 이동 칸이 1인 선형 탐사
+ 특정 해시값 주변에 데이터가 모두 채워져 있다면, 많은 칸 수를 이동해야 하는 문제 발생
* 제곱 탐사(Quadratic probing) : 해시충돌이 일어났을 때, 이동 칸 수가 제곱수로 늘어나며 이동하여 데이터 저장
+ 1차 충돌에는 1의 제곱, 2차 충돌에는 2의 제곱, 3차 충돌에는 3의 제곱 칸 수를 이동
* 이중 해싱(double hashing) : 2개의 해시함수를 사용하여 하나는 해시값을 얻는 데 사용하고, 나머지 하나는 해시 충돌이 일어났을 때 탐사 이동폭을 얻기 위해 사용
+ 예시
~ 해시함수 1은 3으로 나누어 해시값을 얻는 함수
~ 해시함수 2는 5로 나누어 이동 폭을 얻는 함수
~ 키값 3과 6이 오면 해시함수 1에 의해서 둘 다 해시값이 0으로 해시충돌 발생
~ 하지만 해시함수 2에 의해서 키값 6은 1칸 이동하여 저장
- 삽입/삭제/탐색 시간복잡도
* 최악의 경우 : O(n)
+ 모든 bucket을 다 탐색
* 최선의 경우 : O(1)
+ 한 번에 찾음
- 장점
* 메모리 문제 적음
- 단점
* 해시충돌 발생
* chaining 방법과 다르게 해시 테이블의 크기가 고정되어 있기 때문에 어느 정도 칸이 차게 되면 효율성이 떨어지게 된다. 왜냐하면, 탐색/삭제/삽입의 시간복잡도 O(n)으로 도달하기 때문이다. 따라서 75% 정도 칸이 찼다고 하면 해시 테이블의 크기를 늘려고 주고 다시 해싱을 하는 것을 추천한다.
3) 해시함수
- 특정 값에 치우치지 않게 해시값을 만드는 방법
- Division method
* 키값을 테이블의 크기(m)으로 나누는 방법
* m은 일반적으로 소수이며 2의 제곱수와 먼 소수
* 빠름
- multiplication method
* 곱셈으로 해시값을 찾는 방법
* h(k) = m * (k * A mod 1)
* k : 키
* h() : 해시함수
* m : 테이블 크기, 일반적으로 2의 제곱수
* A : 0 ~ 1 사이의 실수
* 2진수 연산에 최적화된 컴퓨터 구조를 고려한 해시함수
- Universal hashing
* 다수의 해시함수를 만들고, 무작위로 선택하여 해시값을 만드는 방법
* 임의의 키값을 임의의 해시값에 매핑할 확률은 1/m으로 만드는 것이 목적
참조
- 위키백과 : ko.wikipedia.org/wiki/%ED%95%B4%EC%8B%9C_%ED%95%A8%EC%88%98
- ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/
'Software Courses > Data Structure' 카테고리의 다른 글
| Graph (0) | 2020.12.21 |
|---|---|
| Tree : Binary tree (0) | 2020.12.20 |
| Heap (0) | 2020.12.19 |
| Priority queue (0) | 2020.12.19 |
| Stack & Queue (0) | 2020.12.13 |