Software Courses/Data Structure

Tree : Binary tree

김 정 환 2020. 12. 20. 19:31
반응형

Tree

    - 하나의 root 노드를 갖음

    - 사이클이 없음

    - 계층적 모델

    - 그래프의 한 종류로, 방향이 있는 연결 그래프

    - N개의 노드와 N-1개의 간선이 존재

 

 

 

용어 표현

    - 루트(root) : 부모가 없는 노드

    - 단말 노드 (leaf) : 자식이 없는 노드

    - 간선 : 노드를 연결하는 선

    - 형제 : 같은 부모를 갖는 노드

    - 차수 : 자식 노드와 연결된 간선의 개수

    - 노드의 크기 : 자신을 포함한 모든 자손 노드의 개수

    - 노드의 깊이 : 루트에서 어떤 노드까지 도달하는 데 가치는 간선의 수

 

 

 

 

 

트리의 종류

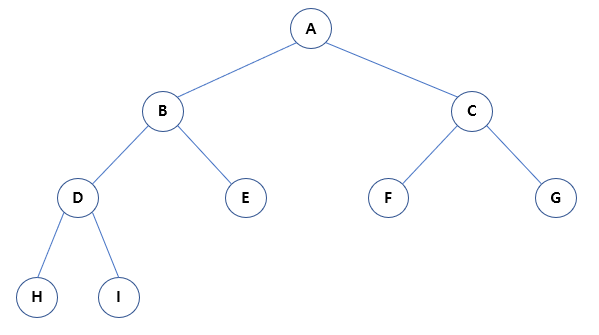
1) 이진 트리

    - 자식 노드 개수(차수)를 최대로 2개를 갖는 트리

 

 

(1) 이진 탐색 트리 (Binary Search Tree)

    - 이진 검색을 위한 구조

    - 왼쪽 서브 트리의 모든 키 값은 부모 노드보다 작음

    - 오른쪽 서브 트리의 모든 키 값은 부모 노드보다 큼

    - 삽입/삭제/탐색의 평균 시간복잡도 : O(logN)

 

    - 문제점

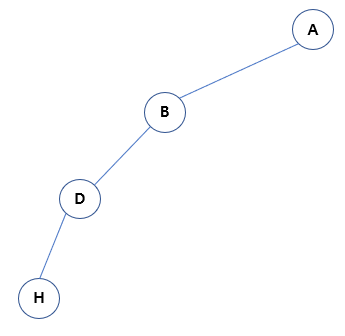
        * 편향 트리 (skewed tree) : 데이터가 한 쪽으로 쏠려서 저장

            + 편향 트리일 경우, 시간복잡도 : O(n)

 

왼쪽 : 편향 트리, 오른쪽 : 완전 이진 트리

 

    - 구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
#include <iostream>
#include <vector>
#include <cstdlib>
 
using namespace std; 
 
// 노드  
typedef struct Node{
    int data;
    Node* left = NULL;
    Node* right = NULL;
}Node;
 
vector<int> bag;
 
// 삽입  
void insert_element(Node* root, Node &node){
    
    // right
    if(node.data > root->data){
        if(root->right == NULL) {
            root->right = &node;
            return;
            
        }else{
            insert(root->right, node);
        }
    }
    
    // left
    else if(node.data < root->data){
        if(root->left == NULL){
            root->left = &node;
            return;
            
        }else{
            insert(root->left, node);
        }
    }
    
    // duplicate
    else {
        cout << "duplicated number" << endl;
    } 
}
 
// 삭제  
void delete_element(Node* root, int data) {
    
    Node *parent, *child, *sub, *sub_p, *t;
    
    parent = NULL;
    t = root;
    
    while(t != NULL && t->data != data){
        parent = t;
        
        if(data > parent->data) t = parent->right;
        else t = parent -> left;
    }
    
    // 찾는 값이 없을 때  
    if(t == NULL){
        cout << "No data" << endl;
        return;
    }
    
    // 찾았는데, 찾은 노드에 자식이 없을 때  
    if(t->left == NULL && t->right == NULL){
        cout << "no children" << endl;
        if(parent){
            if(parent->left == t)
                parent->left = NULL;
            else
                parent->right = NULL;    
        }
        // 지우는 노드가 root일 때  
        else
            root = NULL; 
    }
    
    // 찾았는데 서브 트리가 1개 있을 때
    else if((t->left == NULL) || (t->right == NULL)){
        
        if(t->left != NULL) child = t->left;
        else child = t->right;
        
        if(parent){
            if(parent->left == t)
                parent->left = child;
            else 
                parent->right = child;
        }
        //지우는 노드가 root일 때 
        else
            root = child;
    } 
    
    // 찾았는데 서브 트리가 2개 있을 때
    else{
        //왼쪽 서브 트리에서 가장 큰 값을 찾는다 
        sub_p = t;
        sub = t->right;
        
        while(sub->right != NULL){
            sub_p = sub;
            sub = sub_p->right;
        }
        
        if(sub_p->right == sub)
            sub_p->right = sub->left;
        
        else
            sub_p->left = sub->left;
            
        t->data = sub->data;
        t = sub;
    }
}
 
// 중위 순회  
void in_order(Node* node){
    if(node){
       in_order(node->left);
cout << node->data << endl;
       in_order(node->right);
    }
}
 
// 전위 순회  
void pre_order(Node* node){
    if(node){
cout << node->data << endl;
       pre_order(node->left);
       pre_order(node->right);
    }
}
 
// 후위 순회  
void post_order(Node* node){
    if(node){
       post_order(node->left);
       post_order(node->right);
        cout << node->data << endl;
    }
}
 
 
int main(){
    
    int num;
    while (cin>>num) {
        if (num == EOF) break;
        bag.push_back(num);
    }
    
    vector<Node> nodes;
    
    for(int i=0; i<bag.size(); i++){
        Node node;
        node.data = bag[i];
        node.left = NULL;
        node.right = NULL;
        nodes.push_back(node);
 
    }
    
    Node *root = &nodes[0];
    
    for(int i=1; i<nodes.size(); i++){
        insert_element(root, nodes[i]);
    }
    
    // delete_element(root, 7);
    
    in_order(root);
    pre_order(root);
    post_order(root);
    
    
}
 cs
 
 
  

 

        * 삽입

            + 삽입은 간단

            + 노드보다 크면 오른쪽으로, 노드보다 작으면 왼쪽으로 보낸다.

            + NULL이 나오면 값을 넣어준다.

 

        * 삭제

            + 3가지 경우

                ~ 찾은 노드에 서브 트리가 없을 때

                ~ 찾은 노드에 서브 트리가 1개 있을 때

                ~ 찾은 노드에 서브 트리가 2개 있을 때

            + 서브 트리가 없을 때는 그냥 삭제

            + 서브 트리가 1개 있을 때는 노드를 삭제하고 서브 트리를 부모 노드에 붙임

            + 서브 트리가 2개 있을 때는 왼쪽 서브 트리에서 가장 큰 값을 또는 오른쪽 서브 트리에서 가장 작은 값을 선택하여 지우고자 하는 노드에 넣어주고 삭제

 

            + 경우 3에 대한 추가 설명

                ~ 24를 지우고 싶다. 왼쪽에서 가장 큰 수는 23이다. 20의 오른쪽에 23의 왼쪽 서브트리 22를 붙여준다. 23의 데이터를 24 노드에 넣어준다. 떠돌이가 된 23 노드 메모리는 포인터 t에 담겨지고 메모리가 해체된다.

                ~ 자세한 설명은 이 블로그를 참조하세요.

 

 

 

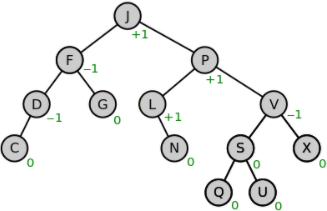
(2) AVL 트리

    - 편향 트리와 같이 균형이 맞지 않는 트리를 균형 트리로 만드는 트리

    - 시간복잡도를 O(logN)으로 유지

 

    - 조건 : 각 노드의 왼쪽 서브 트리와 오른쪽 서브 트리의 높이 차이는 1 이하

출처 : 위키피디아

    - 동작

        * 4 가지의 경우에 따라 재조정 실행

 

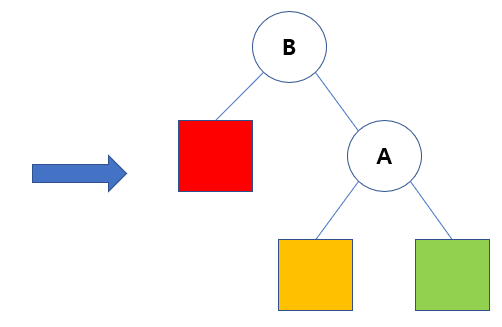
        * 경우 1, 균형이 왼쪽 서브 트리의 왼쪽 서브 트리에 의해 깨진 경우 : LL 회전

            + A를 기준으로 오른쪽으로 회전

 

 

        * 경우 2, 균형이 오른쪽 서브 트리의 오른쪽 서브 트리에 의해 깨진 경우 : RR 회전

            + 경우 1(LL 회전)과 반대

 

 

        * 경우 3, 균형이 왼쪽 서브 트리의 오른쪽 서브 트리에 의해 깨진 경우 : LR 회전

            + B를 기준으로 RR 회전 수행 후 A를 기준으로 LL 회전 수행

 

 

 

        * 경우 4, 균형이 오른쪽 서브 트리의 왼쪽 서브 트리에 의해 깨진 경우 : RL 회전

            + 경우 3 (RL 회전)과 반대

 

 

    - 구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
#include <stdio.h>
#include <stdlib.h>
 
using namespace std;
 
//최대값 찾기 함수
int getMax(int a, int b){
    if(a > b) return a;
    return b;
}
 
 
//노드
typedef struct Node {
    int data;
    int height;
    struct Node* leftChild;
    struct Node* rightChild;
} Node;
 
 
// 높이 구하는 함수  
int getHeight(Node* node){
    if(node == NULL) return 0;
    return node -> height;
}
 
 
// 회전 수행 후에 모든 노드 높이를 재설정
void setHeight(Node* node){
    node->height = getMax(getHeight(node->leftChild), getHeight(node->rightChild)) + 1;
} 
 
 
// 군형 인수 계산 함수
int getDifference(Node *node){
    if(node == NULL) return 0;
    Node *leftChild = node->leftChild;
    Node *rightChild = node->rightChild;
    return getHeight(leftChild) - getHeight(rightChild);
}
 
 
//LL 회전  
Node *rotateLL(Node* node){
    Node *leftChild = node->leftChild;
    node->leftChild = leftChild->rightChild;
    leftChild->rightChild = node;
    // node의 높이만 변경된다.  
    setHeight(node);
    return leftChild;
}
 
 
//RR 회전  
Node *rotateRR(Node* node){
    Node* rightChild = node->rightChild;
    node->rightChild = rightChild->leftChild;
    rightChild->leftChild = node;
    setHeight(node);
    return rightChild;
}
 
 
//LR 회전
Node* rotateLR(Node* node){
    Node *leftChild = node->leftChild;
    node->leftChild = rotateRR(leftChild);
    return rotateLL(node);
} 
 
 
//RL 회전 
Node* rotateRL(Node* node){
    Node* rightChild = node->rightChild;
    node->rightChild = rotateLL(rightChild);
    return rotateRR(node);
} 
 
 
// 균형 맞추기  
Node* balance(Node* node){
    int difference = getDifference(node);
    
    if(difference >= 2){
        // LL, LR 구별
        if(getDifference(node->leftChild) >= 1)
            node = rotateLL(node);
        else 
            node = rotateLR(node); 
    }
    
    else if(difference <= -2){
        // RR, Rl 구별
        if(getDifference(node->rightChild) <= -1)
            node = rotateRR(node);
        else
            node = rotateRL(node);
    }
    
    setHeight(node);
    return node;
}
 
 
// 삽입 함수  
Node* insertNode(Node* node, int data){
    
    if(!node){
        node = (Node*)malloc(sizeof(Node));
        node->data = data;
        node->height = 1;
        node->leftChild = node->rightChild = NULL;
    }
    
    else if(data < node->data){
        node->leftChild = insertNode(node->leftChild, data);
        node = balance(node);
    }
    
    else if(data > node->data){
        node->rightChild = insertNode(node->rightChild, data);
        node = balance(node);
    }
    else {
        printf("duplicated data");
    }
    
    return node;
}
 
 
// 출력 함수
Node* root = NULL;
 
void display(Node* node, int level){
    if(node != NULL){
        //가장 오른쪽 노드부터 방문
        display(node->rightChild, level+1);
        printf("\n");
        
        if(node == root) printf("root : ");
        
        for(int i =0; i<level && node != root; i++)
            printf("      ");
        
        printf("%d(%d)", node->data, getHeight(node));
        display(node->leftChild, level + 1);
        
    }
}
 
 
int main(){
    root = insertNode(root, 7);
    root = insertNode(root, 6);
    root = insertNode(root, 5);
    root = insertNode(root, 3);
    root = insertNode(root, 1);
    root = insertNode(root, 9);
    root = insertNode(root, 8);
    root = insertNode(root, 12);
    root = insertNode(root, 16);
    root = insertNode(root, 18);
    root = insertNode(root, 23);
    root = insertNode(root, 21);
    root = insertNode(root, 14);
    root = insertNode(root, 15);
    root = insertNode(root, 19);
    root = insertNode(root, 20);
    display(root, 1);
    printf("\n");
    system("pause");
    return 0;
}
 
 cs

 

 

 

(3) Red-black tree

    - 편향 트리와 같이 균형이 맞지 않는 트리를 균형 트리로 만드는 트리

    - 시간복잡도를 O(logN)으로 유지

    - Red-black tree는 여기

 

 

 

(4) 완전 이진 트리

    - 트리의 원소는 왼쪽에서 오른쪽으로 차례대로 모두 채워진 상태

    - 왼쪽은 완전 이진 트리, 오른쪽은 완전 이진 트리가 아님

 

 

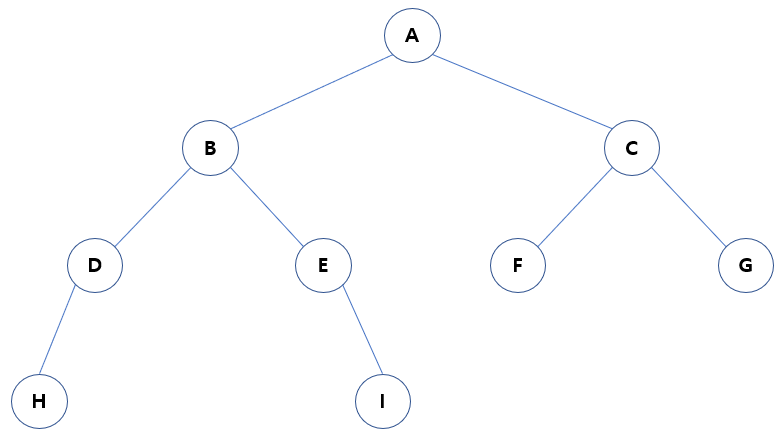
(5) 포화 이진 트리

    - 모든 내부 노드가 두 개의 자식 노드를 가짐

    - 모든 잎 노드가 동일한 깊이 또는 레벨을 가짐

 

 

(6) 힙

    - 여기

 

 

2) B-tree

    - 자식 노드의 개수를 2개 이상 가질 수 있는 트리

    - 노드 내에 데이터가 1개 이상일 수 있고, 정렬되어 있음

    - B-tree는 여기

 

출처 : 위키피디아

 

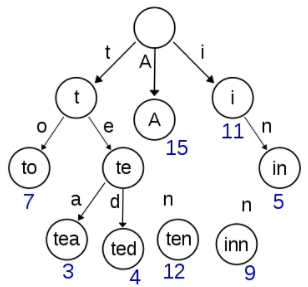
3) 트라이(Trie)

    - 문자열을 저장하고 효율적으로 탐색하기 위한 트리

    - 트라이는 여기

 

출처 : 위키피디아

 

 

사용

    - 목차

    - Unix/Windows의 directory 구조

    - 계층구조에 대부분 사용 가능

 

 

 

참조

    - 블로그 1

    - 블로그 2

    - 블로그 3

    - 위키피디아

    - 나무위키

반응형

'Software Courses > Data Structure' 카테고리의 다른 글

Union-Find  (0) 2020.12.21
Graph  (0) 2020.12.21
Hash table  (0) 2020.12.19
Heap  (0) 2020.12.19
Priority queue  (0) 2020.12.19

'Software Courses/Data Structure'의 다른글

  • 현재글Tree : Binary tree

관련글

댓글

티스토리툴바