This note is based on Coursera course by Andrew ng.
(It is just study note for me. It could be copied or awkward sometimes for sentence anything, because i am not native. But, i want to learn Deep Learning on English. So, everything will be bettter and better :))
When we change our neural network, it's import to initialize the weights randomly. For logistic regression, it was okay to initialize the weights to zero. But for a neural network, initializing the weights to parameters to all zero and then applying gradient descent doesn't work. Let's see why.
The problem with this formalization is that for any example we give it, we will have a[1]1 = a[1]2. It means that all activation functions will be the same. Because these hidden units are computing exactly the same function. And then, when we compute backpropagation, it turns out that dz[1]1 = dz[1]2. By kind of a proof by induction, it turns out that after every single iteration of training our hidden units are still computing exactly the same function.

dw will be a matrix that looks like that. Where every row takes on the same value. So we perform a weight update, after every iteration, we find that w1 will have the first row equal to the second row. Because all hiden units start off computing the same function. And all hidden units have the same influence on the output unit. So, there is no point to having more than on hidden unit.

The solution to this is to initialize our parameters randomly. b doesn't have symmetry breaking problem. So it's okay to initialize b to just zeros. Because so long as w is initalized randomly, we start off with the different hidden units computing different things. And we no longer have this symmetry breaking problem.
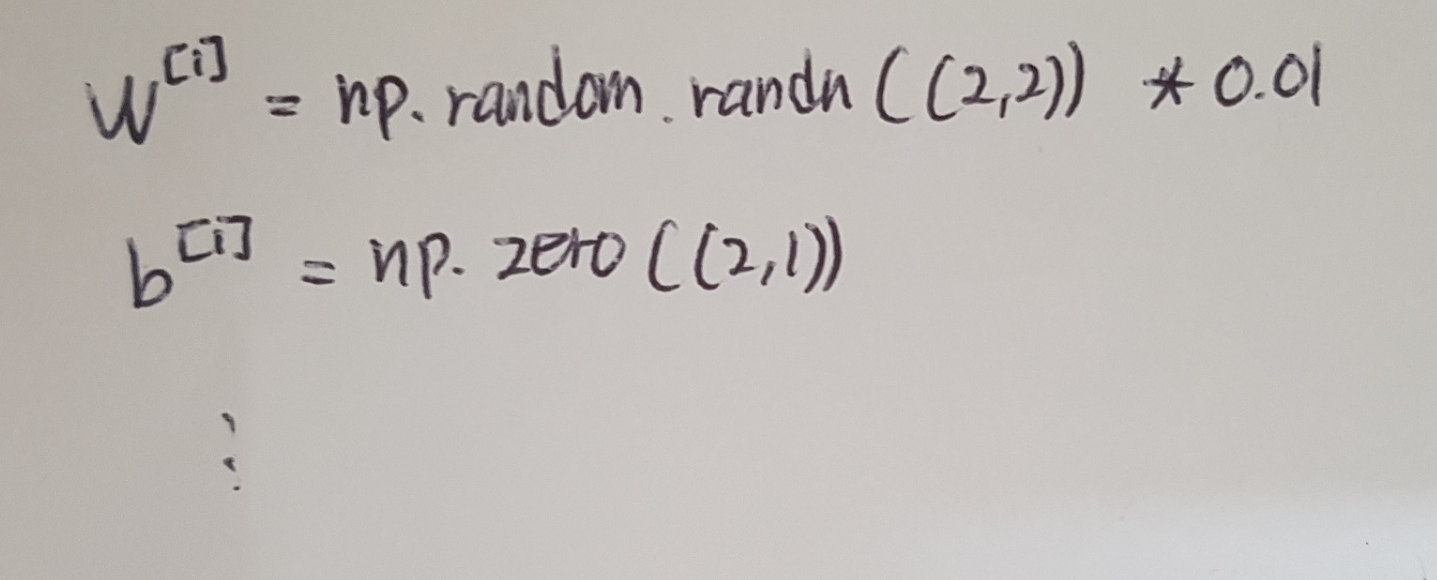
We might be wondering where this constant 0.01 comes from and why it is? We ususally prefer to initialize the weights to very small random values. Because if we are using a tanh or sigmoid activation function and the weights are too large, values of z will be either very large or small. And in that case, we are more likely to end up at these away parts of the activation function. Finally, the slope or gradient is very small, and then gradient descent will be very slow, meaning learning will be very slow.
