[Improving: Hyper-parameter tuning, Regularization and Optimization] Programming - Gradient Checking

This note is based on Coursera course by Andrew ng.

(It is just study note for me. It could be copied or awkward sometimes for sentence anything, because i am not native. But, i want to learn Deep Learning on English. So, everything will be bettter and better :))

 

 

INTRO

To be clear that our backward propagation is correct, we are going to use gradient checking.

 

Backpropagation computes the gradients ∂J/∂θ, where θ denotes the parameters of the model. J is computed using forward propagation and loss function.

 

Definition of derivative: 

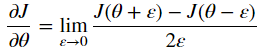
The following figure describes the forward and backward propagation.

 

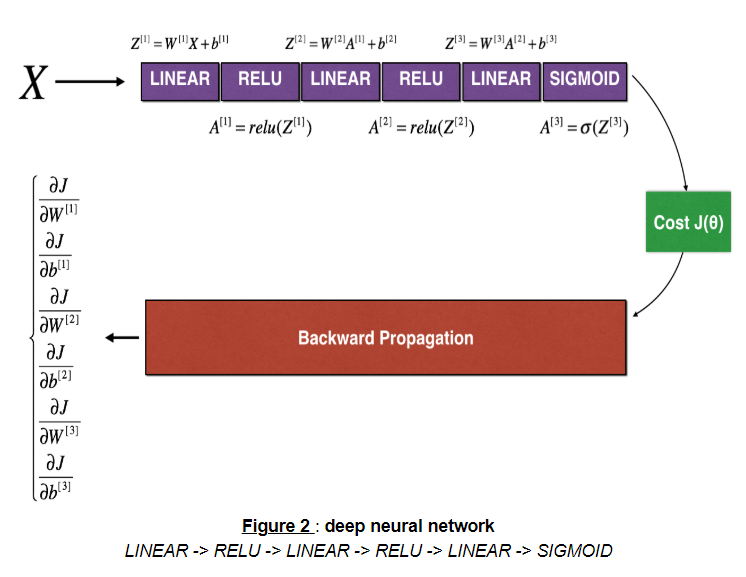
MAIN

Let's look at forward propagation and backward propagation.

def forward_propagation_n(X, Y, parameters):
    """
    Implements the forward propagation (and computes the cost) presented in Figure 3.
    
    Arguments:
    X -- training set for m examples
    Y -- labels for m examples 
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape (5, 4)
                    b1 -- bias vector of shape (5, 1)
                    W2 -- weight matrix of shape (3, 5)
                    b2 -- bias vector of shape (3, 1)
                    W3 -- weight matrix of shape (1, 3)
                    b3 -- bias vector of shape (1, 1)
    
    Returns:
    cost -- the cost function (logistic cost for one example)
    """
    
    # retrieve parameters
    m = X.shape[1]
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
 
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)
 
    # Cost
    logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
    cost = 1./m * np.sum(logprobs)
    
    cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
    
    return cost, cache
 

 

def backward_propagation_n(X, Y, cache):
    """
    Implement the backward propagation presented in figure 2.
    
    Arguments:
    X -- input datapoint, of shape (input size, 1)
    Y -- true "label"
    cache -- cache output from forward_propagation_n()
    
    Returns:
    gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables.
    """
    
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    dW3 = 1./m * np.dot(dZ3, A2.T)
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
    
    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1./m * np.dot(dZ2, A1.T) * 2
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
    
    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1./m * np.dot(dZ1, X.T)
    db1 = 4./m * np.sum(dZ1, axis=1, keepdims = True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
                 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
                 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients
 

 

θ is not a scalar. It is a dictionary called 'parameters'.

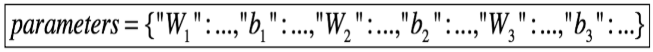
We implemented a function 'dictionary_to_vector()'. It converts the 'parameters' dictionary into a vector. And inverse function is 'vector_to_dictionary' which outputs back the 'parameters' dictionary.

 

Finally, compute the relative difference between 'gradapprox' and the 'grad' using the following formula.

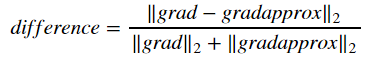
We will need 3 steps to compute this formula:

• compute the numerator using np.linalg.norm(...)
• compute the denominator. You will need to call np.linalg.norm(...) twice.
• divide them.

 

def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):
    """
    Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
    
    Arguments:
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
    grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters. 
    x -- input datapoint, of shape (input size, 1)
    y -- true "label"
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient
    """
    
    # Set-up variables
    parameters_values, _ = dictionary_to_vector(parameters)
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))
    
    # Compute gradapprox
    for i in range(num_parameters):
        
        # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
        ### START CODE HERE ### (approx. 3 lines)
        thetaplus = np.copy(parameters_values) # Step 1 : copy parameters_values
        thetaplus[i][0] = thetaplus[i][0] + epsilon                                      # Step 2 : add epsilon to each value(theta and bias)
        J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus))     # Step 3 : compute cost
        ### END CODE HERE ###
        
        # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
        ### START CODE HERE ### (approx. 3 lines)
        thetaminus = np.copy(parameters_values) # Step 1
        thetaminus[i][0] = thetaminus[i][0] - epsilon                                     # Step 2        
        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus))    # Step 3
        ### END CODE HERE ###
        
        # Compute gradapprox[i]
        ### START CODE HERE ### (approx. 1 line)
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2*epsilon)
        ### END CODE HERE ###
    
    # Compare gradapprox to backward propagation gradients by computing difference.
    ### START CODE HERE ### (approx. 1 line)
    numerator = np.linalg.norm(gradapprox - grad)                                           # Step 1'
    denominator = np.linalg.norm(gradapprox) + np.linalg.norm(grad) # Step 2'
    difference = numerator / denominator                                           # Step 3'
    ### END CODE HERE ###
 
    if difference > 2e-7:
        print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
    else:
        print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
    
    return difference
 
 

 

shape of prameters and parameters_values: 

• parameters : {'W1': array([[-0.3224172 , -0.38405435, 1.13376944, -1.09989127], [-0.17242821, -0.87785842, 0.04221375, 0.58281521], [-1.10061918, 1.14472371, 0.90159072, 0.50249434], [ 0.90085595, -0.68372786, -0.12289023, -0.93576943], [-0.26788808, 0.53035547, -0.69166075, -0.39675353]]), 'b1': array([[-0.6871727 ], [-0.84520564], [-0.67124613], [-0.0126646 ], [-1.11731035]]), 'W2': array([[ 0.2344157 , 1.65980218, 0.74204416, -0.19183555, -0.88762896], [-0.74715829, 1.6924546 , 0.05080775, -0.63699565, 0.19091548], [ 2.10025514, 0.12015895, 0.61720311, 0.30017032, -0.35224985]]), 'b2': array([[-1.1425182 ], [-0.34934272], [-0.20889423]]), 'W3': array([[ 0.58662319, 0.83898341, 0.93110208]]), 'b3': array([[ 0.28558733]])}
• parameters_values: [[-0.3224172 ] [-0.38405435] [ 1.13376944] [-1.09989127] [-0.17242821] [-0.87785842] [ 0.04221375] [ 0.58281521] [-1.10061918] [ 1.14472371] [ 0.90159072] [ 0.50249434] [ 0.90085595] [-0.68372786] [-0.12289023] [-0.93576943] [-0.26788808] [ 0.53035547] [-0.69166075] [-0.39675353] [-0.6871727 ] [-0.84520564] [-0.67124613] [-0.0126646 ] [-1.11731035] [ 0.2344157 ] [ 1.65980218] [ 0.74204416] [-0.19183555] [-0.88762896] [-0.74715829] [ 1.6924546 ] [ 0.05080775] [-0.63699565] [ 0.19091548] [ 2.10025514] [ 0.12015895] [ 0.61720311] [ 0.30017032] [-0.35224985] [-1.1425182 ] [-0.34934272] [-0.20889423] [ 0.58662319] [ 0.83898341] [ 0.93110208] [ 0.28558733]]

 

If we see the gradient checking, it ouputs 0.285093156781. It means there is a mistake in the backward propagation. Then if we checked backward_propagtaion_n function, we can find dW2 multiply with 2 and db1 multiply with 4. So, change them to 1. And if we execute gradient checking again, we will get 1.18855520355e-07 difference.   

 

 

 

 

CONCLUSION

Remind 

• Gradient checking verifies closeness between the gradients from backpropagation and the numerical approximation of the gradient.
• Gradient checking is slow because of computing approximation of the gradient. So we run it only to make sure back propagtaion(gradient) is corrent.
• Gradient checking doesn't work with dropout. So, we run the gradient checking without dropout to make sure backpropagation is correct.