This note is based on Coursera course by Andrew ng.
(It is just study note for me. It could be copied or awkward sometimes for sentence anything, because i am not native. But, i want to learn Deep Learning on English. So, everything will be bettter and better :))
INTRO
One of the problems of training neural network, especially very deep neural networks, is data vanishing and exploding gradients. It means that when training a very deep network, derivatives or slopes can sometimes get either very big or very small.
MAIN
We are training a very deep neural network like this. For the sake of simplicity, we are using an activation function g(z) = z, which is linear activation function, and b = 0. So, in that case we can show that the ouptut y_hat will be w[l]w[l-1]w[l-2]w[l-3] ... w[2]w[1]x.

Now, each of weight matrices w[l] is a little bit larger than one. y_hat will be like this below. And if L is very large, y_hat will be very large. It grows exponentially. So, if we have a very deep neural network, the value of y_hat will explode.
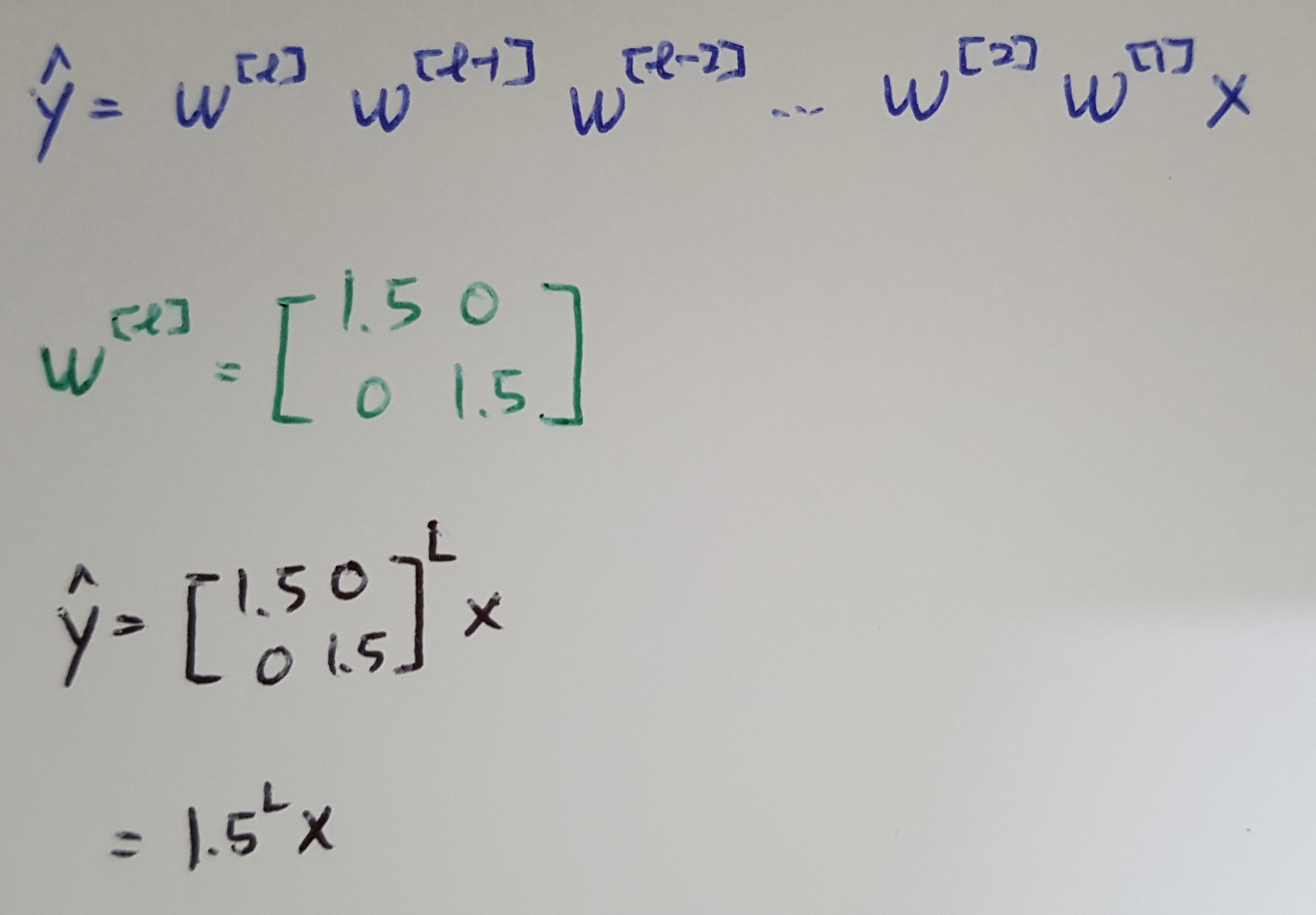
Conversely, if we replace this 1.5 with 0.5, activations end up decreasing exponetially. 0.5^L * x.
Solution : set the variance of weight initialization to be 1/n
Here is a signle neuron, and then we will talk about the deep net later. If we are adding up a lot of these w[i]x[i], we want each of these to be smaller because we worry that z will be bigger.
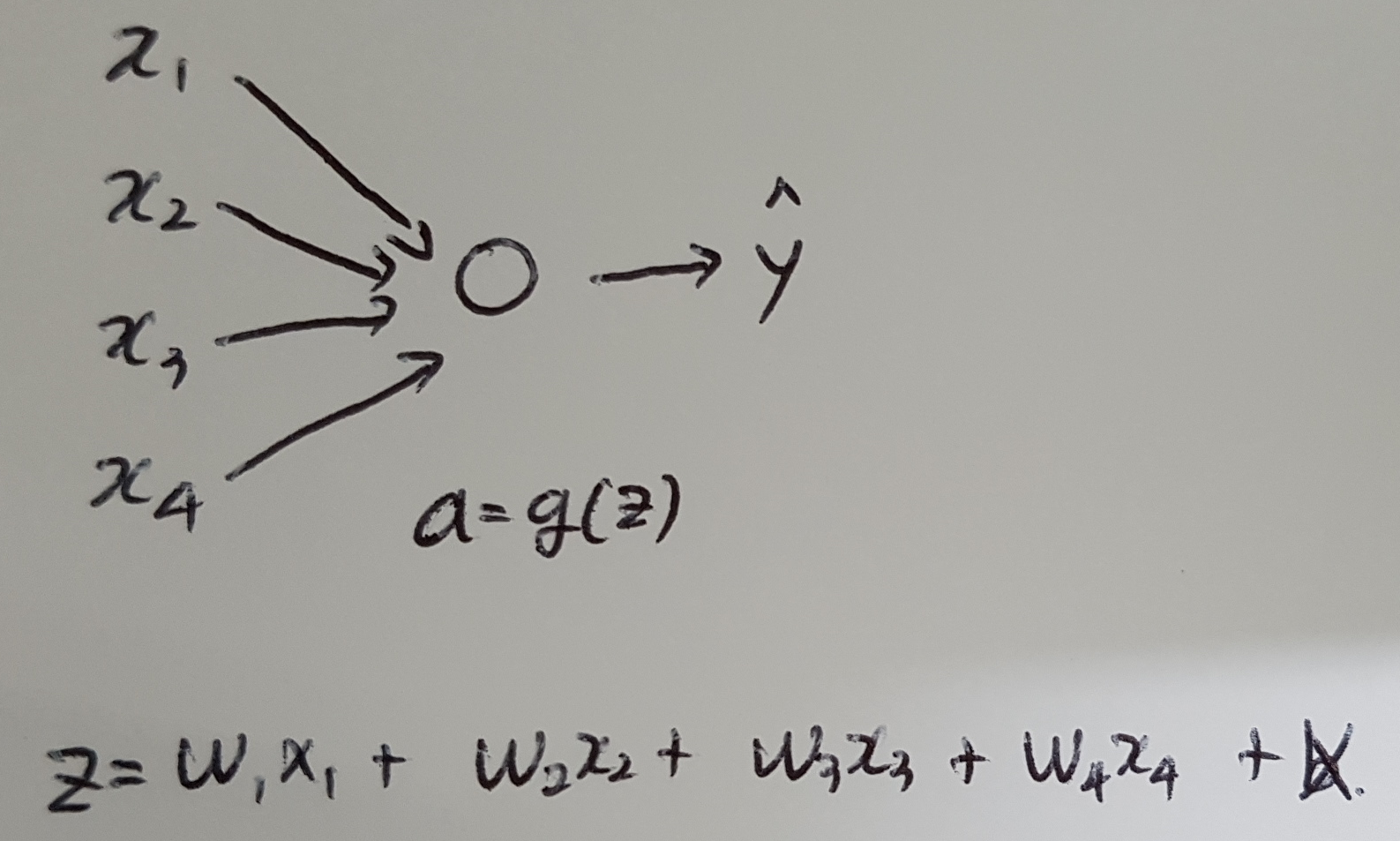
One reasonable thing to do would be to set the variance of w[i] to be equal to 1/n, where n is the number of input features that is going into a neuron. It is not a absolute solution but helps reduece the vanishing and exploding gradients problem. Because it tries to set each of the weight matrices w so that it is not too much bigger than 1 and not too much less than 1, then it doesn't explode or vanish too quickly.
(n[l-1] comes from last layer because the number of units that we feed into each of the units in layer l.)

If we use Tanh activation function, we use Xavier initialization.

CONCLUSION