This note is based on Coursera course by Andrew ng.
(It is just study note for me. It could be copied or awkward sometimes for sentence anything, because i am not native. But, i want to learn Deep Learning on English. So, everything will be bettter and better :))
INTRO
Sometimes we write all back prop equations and we are just not 100% sure if we have got all the details right and internal back propagation. When we implemet back propagation, we will find that there is a test called gradient checking that can really help us make sure that implementation of back prop is correct.
MAIN
1. Take W[1], b[1], ..., W[L], b[L] and reshape into a big vector θ. So, we can write J to this like below.
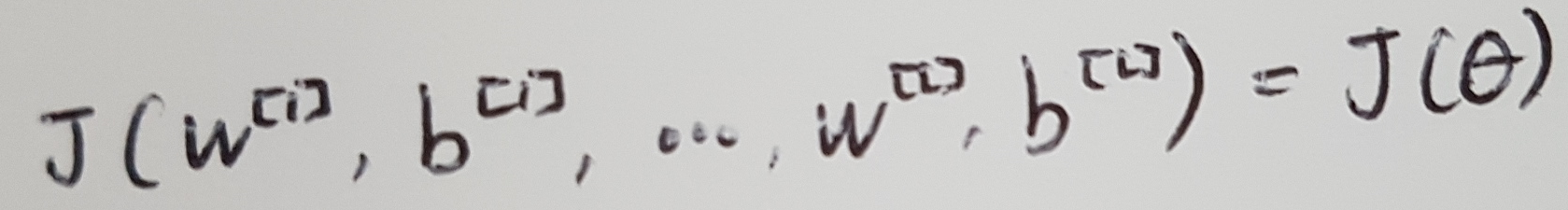
2. Take dW[1], db[1], ..., dW[L], db[L] and reshape into a big vector dθ.
3. Is dθ equal to the gradient of J?

To define whether or not two vectors are really reasonably close to each other, we compute the euclidean distance between these two vectors. dθ_approx - dθ. And then, nomalize by the lengths of these vectors by dividing by dθ_approx + dθ.

Practical tips
1. Don't use in training - only to debug
- Computing dθ is very slow. So, once you have done gradient checking, then you would turn off the gradient checking, and don't run this during every iteration of gradient descent.
2. If algorithm fails grad check, look at component to try to identify bug.
- If dθ_approx[i] is very far from dθ[i], you look at the different values of i to see which are the valures of dθ_approx that are really very different than the values of dθ.
3. Remember regularization.
- Don't forget to include regularization term when you compute dθ_approx.
4. Doesn't work with dropout.
- The cost function J defined by summing over all exponetially large subsets of nodes they could eliminate in any iteration. So the cost function J is very difficult to compute.
- Set keep_prob = 1.0
5. Run at random initialization; perphaps again after some training.
- Implementation of gradient descent is correct when w and b are close to 0, at random initialization. But as you run gradient descent and w and b become bigger, it gets more inaccurate when w and b become large.
- So, run gradient checking at random initialization and run gradient checking again after you have trained for some number of iterations.
CONCLUSION